咳咳,这篇短文继续讲统计。(老实说,下面的内容比较严肃与难懂,如果你觉得实在太晦涩,建议放弃吧,我们之间是不可能的)
学过统计的都知道,统计方法如单样本检验、双样本检验、方差分析都有公式直接计算。然而SPM,FSL等软件里的统计用的广义线性模型,而不是统计公式。因为在某些情况下,直接用统计公式行不通。比如想要在控制一个变量的条件下,比较两组数据的均值差异。这种情况下,直接使用双样本公式行不通,需要广义线性模型来求解。
广义线性模型公式: Y = AX。Y是因变量,X是自变量,A是设计矩阵。可以这么说,几乎所有的统计都可以用广义线性模型来描述。那么怎么理解广义线性模型呢?
理解广义线性模型关键是理解两个概念:设计矩阵和对比矩阵。
设计矩阵是一个n×m的矩阵,n表示的是观测值个数(比如被试个数),m表示自变量个数(每一列代表一个自变量)。如下图:这是一个5x4的设计矩阵,表示有5个观测值(5个被试),有4个自变量(比如第一列到第四列分别是:年龄、性别、教育年限、智商)
对比矩阵是一个p×m的矩阵(这里只讨论最简单的情形,1×m对比矩阵)。一个对比矩阵对应一个统计假设。比如说我们想关注,排除其他自变量的影响下,年龄和因变量(比如ALFF)的关系,那么对比矩阵就是[1 0 0 0],其中1表示我们关注的这个变量(年龄),0表示我们需要回归掉的变量。再比如对比矩阵 [0 1 0 0]表示排除年龄、教育年限和智商的情况下,看性别对因变量的作用。
下面我们从实际例子来理解设计矩阵和对比矩阵。
我们从最简单的单样本检验和双样本检验说起。这里有个假设,即是数据服从正态分布。
下面会有一些简单的公式和数学符号,当然也可以跳过这些公式,直接看图和说明也可。
(1)单样本检验
有一组服从均值为μ,方差为σ的正态分布数据,单样本检验是检验这一组数据均值是否等于0.即是检验μ是否为0.我们从广义线性模型角度出发来理解。首先画出正态分布图:
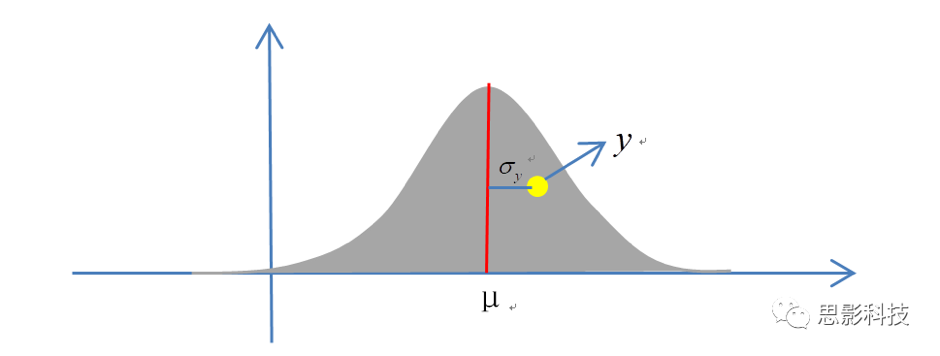

那么单样本检验的设计矩阵A就是一列1(在本例中是3x1的矩阵),这一列1代表了这一组数据的均值(我们可以把这个概念推广,如果设计矩阵里有一列全为1的,那么这一列代表的是所有数据总的均值)。如果我们要检验这组数据均值是否等于0,那么它的对比矩阵只有一个数,即1.
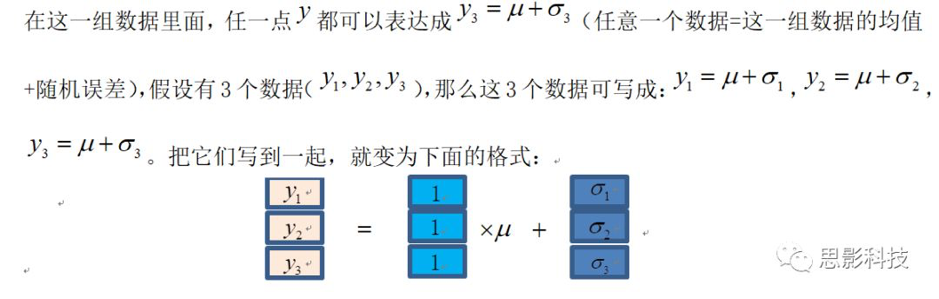
这时候如果我们想加入一个协变量-年龄。假设三个被试的年龄分别是29,31,28。那么就变为下面的格式:

这时候设计矩阵A是一个3x2的矩阵(请自行目测哪一个是设计矩A),3表示有3个观测值(3个被试),2表示有2两个自变量,分别是这一组数据的均值(μ)和年龄(age)。如果我们想看在回归年龄的情况下,检验这一组数据的均值是否为0,对比矩阵是[1 0]。如果想看年龄和这一组数据的关系,对比矩阵是[0 1]。好,那么对比矩阵[1 -1]表示的是什么呢?没有意义!!!所以对比矩阵一定要根据自己的假设来设置。
作业:请自行使用SPM做单样本统计检验,解释SPM出来的设计矩阵以及设置对应的对比矩阵。
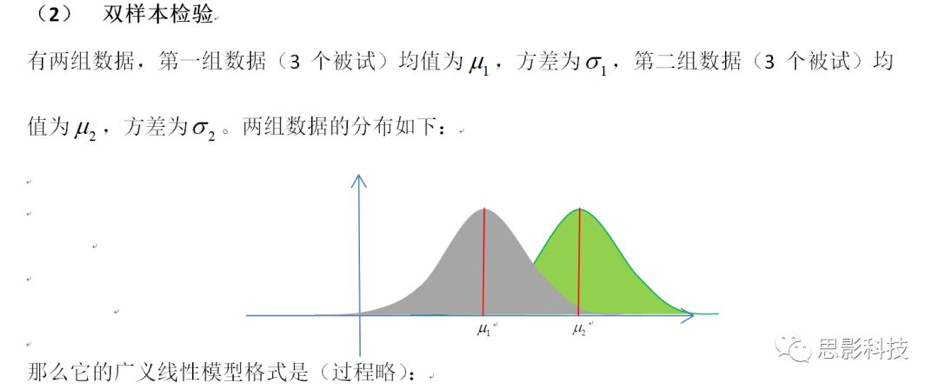
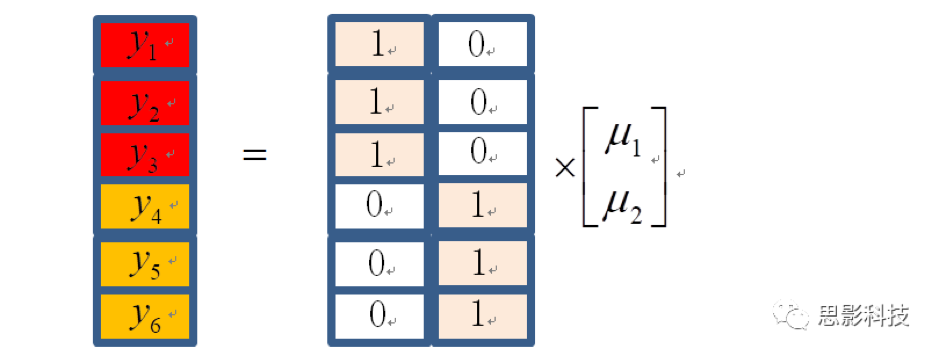
这里省略误差项。右边前三个红色的值是第一组数据,后三个值是第二组数据。这里双样本t检验的设计矩阵是一个6x2的矩阵,6代表总共6个被试。2表示两个自变量(对应两列),第一列是第一组的均值(因为第一列前三个数值是1,后三个是0),第二列是第二组的均值(因为第二列前三个数值是0,后三个数值是1)。那么检验两组均值差异,对比矩阵是[1 -1]。那么[1 0]表示检验组一的均值是否为0,[0 1]表示检验组二均值是否为0。
如果我们想回归掉年龄,这时候设计矩阵就变为三列,前两列不变,第三列是年龄。
思考:如果把年龄变量加进来,检验年龄和组之间的交互,该设计矩阵是什么格式?
讲到这里,大家理解了设计矩阵和对比矩阵了吗?
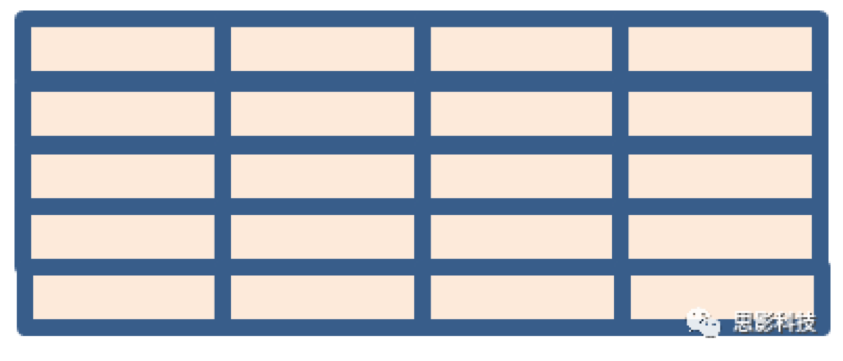
下面列举其它几种统计方法的设计矩阵:
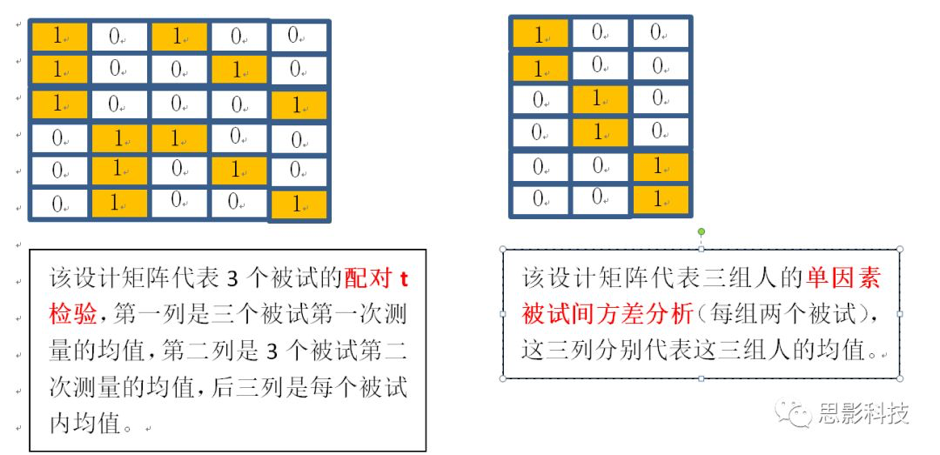
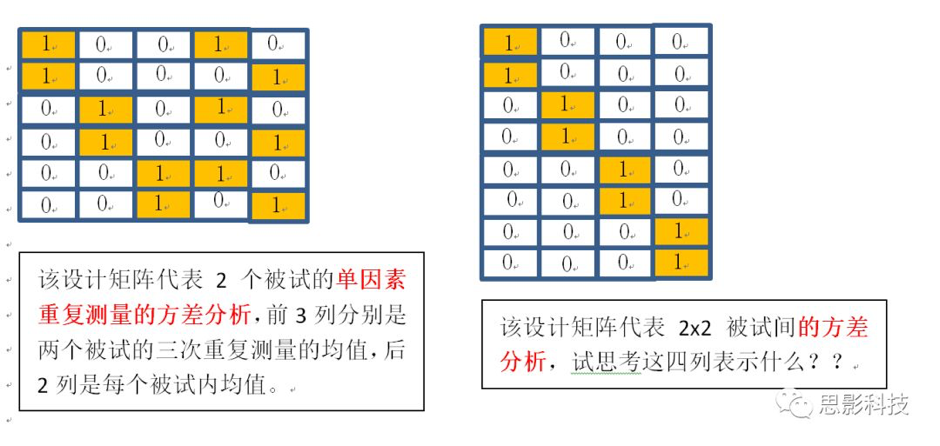
------------------
附注:
1. SPM中,可在Results一步查看设计矩阵并定义Contrast,也可以在Contrast manager中进行。
2. 单样本T检验中,[1 -1]没有意义:均值和年龄(协变量)所做比较无意义。
3. 加入年龄后,设计矩阵格式:
|
1
|
0
|
Age1
|
|
|
1
|
0
|
Age2
|
|
|
1
|
0
|
Age3
|
|
|
0
|
1
|
0
|
Age4
|
|
0
|
1
|
0
|
Age5
|
|
0
|
1
|
0
|
Age6
|
4. 2*2被试间方差分析,四列代表:组1被试在情况1下的均值,组1被试在情况2下的均值,组2被试在情况1下的均值,组2被试在情况2下的均值。
说了这么多,也不知道大家掌握没有,正如伟大的鲁迅先生曾经说过:“努力
学好数学,更好的进行脑影像的研究!”,希望大家还是多把数学学好,没准除了搞脑影像研究外,顺便拿个诺贝尔奖啥的(诺贝尔是没有数学奖的,知道为什么吗?据说是因为爱情)

如果你觉得自学很困难,我在重庆等你:
第六届功能磁共振数据处理基础班
适合基础比较薄弱的朋友,起步开始想做脑影像研究的朋友(没错,直接点击,不用犹豫)
第三届磁共振脑网络数据处理班
适合已经有一定基础,想挑战自己的朋友
第二届磁共振DTI(弥散张量成像)数据处理班
适合想专攻DTI的朋友,由浅入深,相信我学完之后无论你是想做基本的确定追踪,纤维束骨架还是挑战复杂的概率追踪及DTI脑网络,你都会有所收获。

微信扫码关注,这么用心的公众号,不是俗物。
祝所有关注者,新春愉快!