少年，我看你骨骼精奇，是万中无一的武学奇才，维护世界和平就靠你了，我这有本武林秘籍《九阴真经之万军丛中听声辩位分筋错骨取敌将首级之盲源分离大法》，简称，《独立成分分析》，见与你有缘，转发一下就送给你了！

       我们在听力上与生俱来就有从混合信号中提取源信号的能力。设想你身处一个热闹的鸡尾酒会，各路名流谈笑风生，孩童嬉戏打闹，顶级乐队高山流水，这时候隔壁工地的工头在远处喊了一声你的名字：李狗蛋！瞬间就穿透其他声音传入你的耳朵，你只好悻悻回去，在工头的呵斥下与赛琳娜告别，悻悻回去搬砖。这就是鸡尾酒会效应（英语：cocktail party effect），它指人的一种听力选择能力，在这种情况下，注意力集中在某一个人的谈话之中而忽略背景中其他的对话或噪音。该效应揭示了人类听觉系统中令人惊奇的能力，使我们可以在噪声中谈话。在数学上，我们将一系列混合信号解码成一系列源信号的方法叫做盲源分离（BSS，blind source seperation），而独立成分分析（ICA，independent component analysis）就是一种典型的盲源分离的方法。

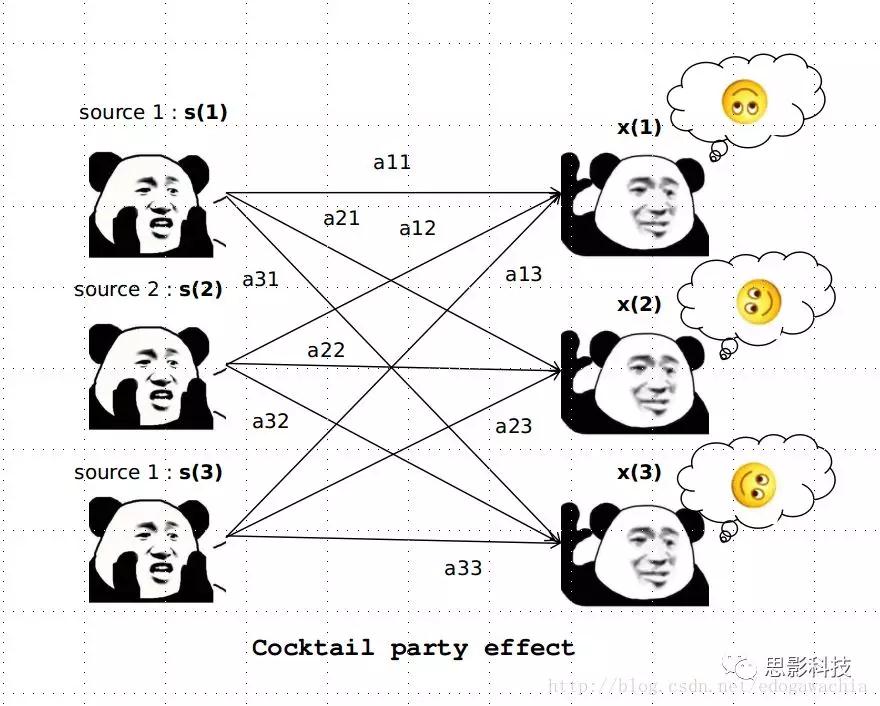
     前文提到李狗蛋在酒会中分辨出工头声音，有很大一部分原因是他原先就知道工头的声音的特征，而计算机并不知道源信号的特征具体是什么样的，此时我们就需要多个观测数据（比如在n个人说话的房间不同位置放m个话筒），并且我们需要m>n（即话筒数需要大于说话的人数）。这涉及到矩阵求解中的超定和欠定问题，在此不做赘述。本文作为一档严（you）肃（mo）而不正经的科普文，接下来我需要列一下公式：

假设某个数据  是由 n 个独立的数据源而产生的。我们观察到的是：

x = As

这里矩阵 A 是方阵，被称作混合矩阵。观察或者记录 m 次，就可以得到一个数据集{x(i); i = 1, 2, ... , m}，我们的目标是利用已经产生的数据( x(i) = As(i) )去恢复出数据源 s(i)。

     细心的同学可以已经发现了，上式中，只有观测信号x是我们已知的，而混合矩阵A和源信号矩阵s对于我们都是未知的。学过九年制义务教育这种顶级学历水平的我们知道，只有一个等式是没法求出两个未知数的，此时A和s可以有无穷多个解。所以我们需要加入更多的限制条件来对其进行约束。这里引入一个中心极限定理（Central Limit Theorem）的概念，在适当的条件下，大量相互独立随机变量的均值经适当标准化后依分布收敛于正态（高斯）分布。简单来说，越是混合的变量，越是高斯（高斯性越强）。那我们在一起反向思考就可以发现，越是独立的变量，非高斯性就会越强。如果我们再假设我们的源信号都是相互独立的，再用峭度（kurtosis）等参数对变量的非高斯性进行量化，那么只要找到非高斯性最强的一组相互正交的变量集s，就是我们要求得的原始信号了！这就是ICA的基本原理。具体的ICA优化算法有很多，基于定点递推算法（fixed-point algorithom）的fastICA、基于最大联合熵和梯度算法的Informax以及最大似然估计法（MLE，Maximum likelihood estimation）等，在此就不一一赘述了。

       接下来就是ICA在fMRI中的应用了。由第十期大话脑成像我们知道，fMRI数据是一个四维数据（三维空间加一维的时间）；由于四维空间比较难以想象，为了便于想象，我们先以下图的方式将一个三维的矩阵重新排列成一个一维的向量。

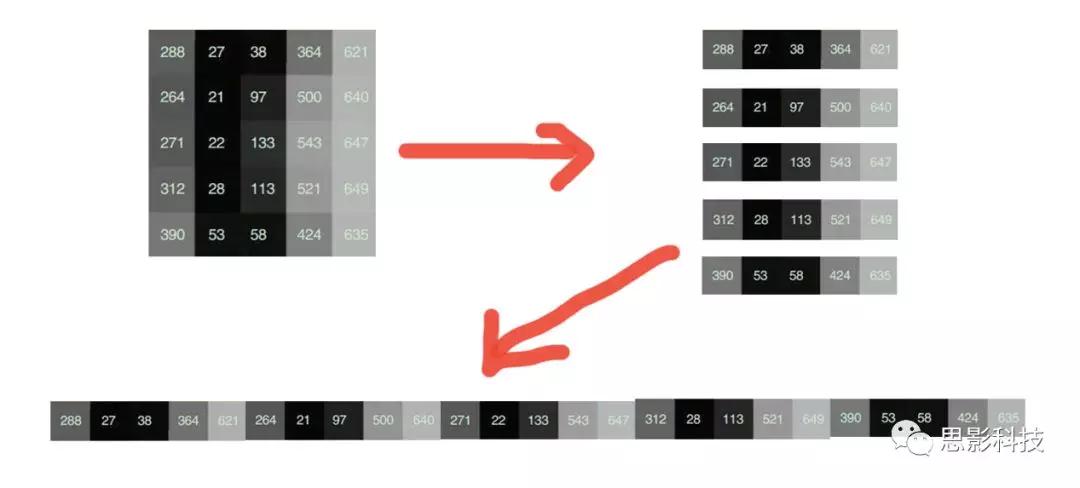
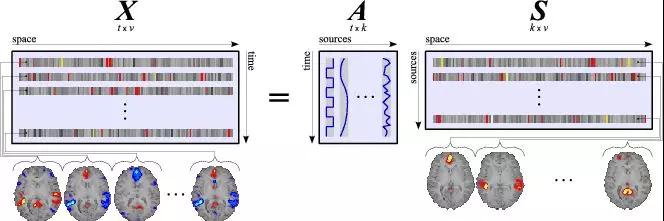
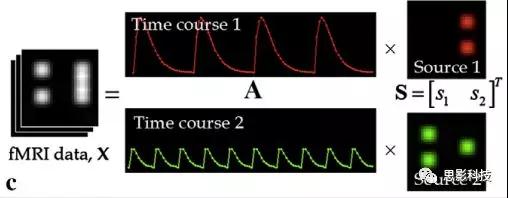
假设我们包含v个体素fMRI数据，时间点为t个，该数据包含k个相互独立源信号，我们的四维fMRI数据就可以表示成一个时间（time）*空间（space）的t*v的二维矩阵，在ICA中，这也是我们的观测信号矩阵x（下图等式最左）；而我们要求解的源信号s矩阵则为源信号成分（source）*空间（space）的k*v的矩阵（下图等式最右），即每个成分的空间分布图；而每个成分的时间序列，即时间（time）*源信号成分（source）的t*k的矩阵（下图等式最右），则为混合矩阵A。

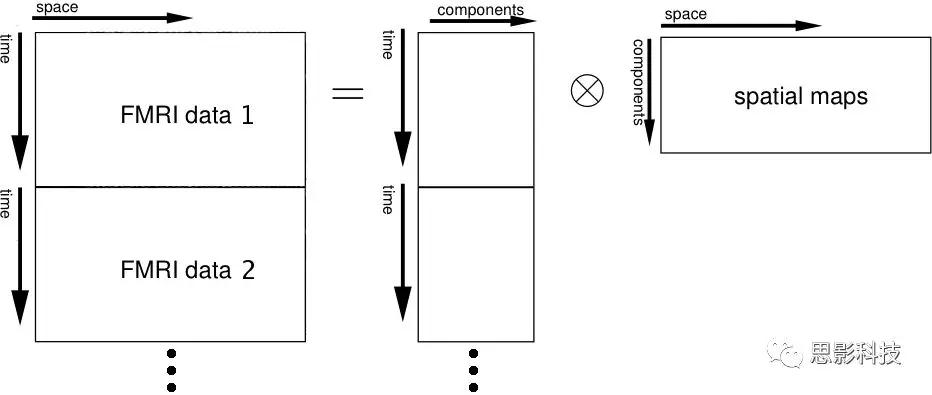
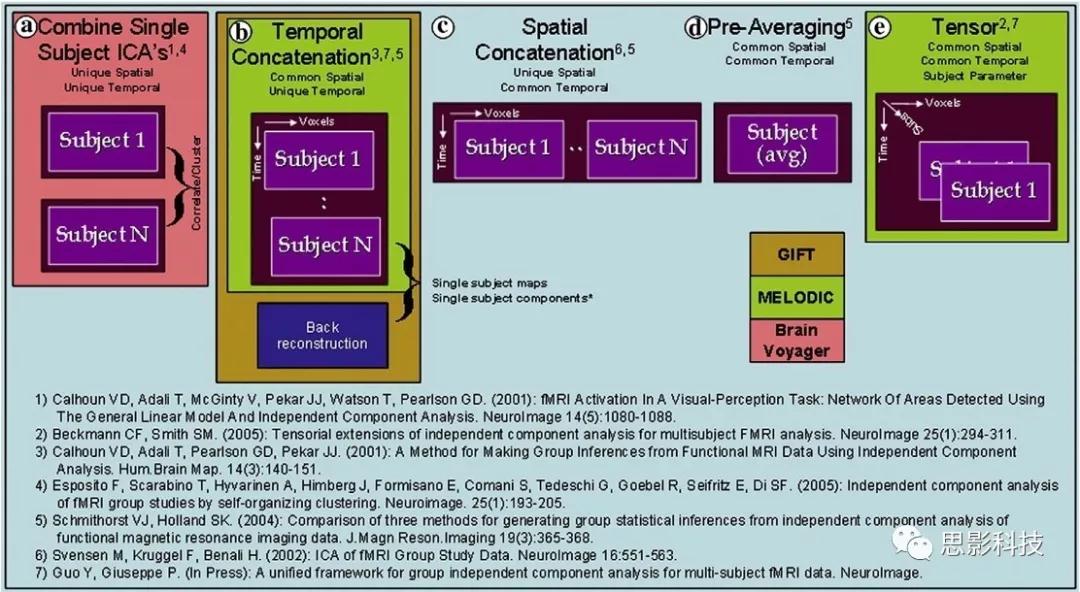
以上是在个体水平上进行ICA的分析。为了找到一组人共同的成分，并在组水平上进行统计比较，我们往往对一整组被试的标准化数据进行时间上的拼接后再进行group ICA的分析，如下图所示。

当然进行group ICA的方法有很多，时间上拼接只是其中一种比较常用的方法。下图分别展示了五种不同的方法以及相应的工具包：

a.单个被试水平计算ICA；

b.时间上拼接个体fMRI；

c.空间上拼接个体fMRI；

d.组水平平均；

e.张量-ICA（原始数据不拼接，为被试*时间*空间三维数据）。

     最后谈一谈笔者常常被问到的一个问题问题以及笔者自己对此的理解：ICA与功能连接的关系。如下图所示，我们假设有一个简单的fMRI数据，它包含两个源信号成分，第一个成分（Source 1）在两个体素上的分布强度值很高，在其他体素上几乎没有分布（图右上）；且别的成分在这两个体素上的分布强度值很低（由于源信号是相互独立的，所以这一点必然满足）；那么这两个体素的时间序列必然高度相关于混合矩阵的同一个也就是第一个时间序列（Time Course 1），它们之间也必然高度相关，即该两个体素间功能连接高度相关，即统一成分内的体素间必然具有高度的功能连接。返回来在个体水平的统计上（此处特指gift统计），如果同一成分（如DMN）在两个组被试的空间分布强度在个别体素区域（如PCC）有显著差异，我们也可以理解为，两组被试的该体素区域（如PCC）与该成分（如DMN）内部其他体素的功能连接强度有显著差异。

文末：今晚世界杯开始，让我预祝下我心中浩气长存的欧洲之花无冕之王大荷兰队顺利夺冠！

哦，对了，差点忘记发广告，广告也精彩（直接点击下文帅气的意大利蓝（目测本届亚军））：

 招聘公告：脑影像数据处理工程师2名（可能是东半球你所能找到的最好的公司，快点拿你的简历砸我，不要逼我上印度智联招聘）

第八届功能磁共振数据处理基础班（这里有本文内容的详解，适合想要开始脑影像数据处理这段神奇旅程的你）

第四届磁共振弥散张量成像数据处理班（让我们一起tra起来！）

第三届磁共振脑影像结构班（多模态必备，学会可以上王者）

第二届磁共振ASL（动脉自旋标记）数据处理班（目前最火的新序列，GPS必争之地，卒中研究必备，良心安利）

第一届动物磁共振脑影像数据处理班（打野玩家乐园，马上开车，速度报名上车）

第一届功能磁共振提高班（学成之后，你可以凭借任务态独门秘籍，独步武林）

思影数据处理业务一：功能磁共振（fMRI）数据处理（皇家思影出品，必属精品）

思影数据处理业务二：结构磁共振成像(sMRI)与弥散张量成像(DTI)处理业务(同上）