前言：该文转自“懋式百科全书”，作者李懋，飞利浦磁共振首席培训工程师，工作出差培训，全国满天飞，坐飞机如打的士的优质精英商务男士。

       在这里提出一个疑问，希望能够得到读者的回答：该作者的相貌平平无奇，为何可以写出如此惊世骇俗之文章？

说到磁共振成像，就不得不提起拍摄1982年西游记时我无意中看到的一个公众号：懋式百科全书，如果你同时关注了思影科技与下文扫码得到的公众号，你就同时获得了成像物理原理与后处理技术的双倍加成，文体两开花，中美合拍，弘扬影像文化。

微信扫码点击，走上人生巅峰！

以下是原文全文，慢慢享用，拿走不谢：

这次我们要来聊聊一个看起来高大上，又悬而又悬的名词——“K Space”，K空间。可能有很多才接触磁共振的同仁，很不愿意去讨论这个名词，因为它听起来飘忽不定，高深莫测。

    K空间为什么要叫K空间，不叫A空间，D空间？这个笔者才疏学浅没有明确的考证出证据。大家只需要记住，K空间其实是频率空间，是以频率空间为坐标系的MR图像原始数据的承载空间。K空间又可以叫傅里叶空间。

    这里讲K空间，就不得不多提一下傅里叶变换（Fourier Transform,  FT）。

    傅里叶变换是一种数学运算方法，简单来讲就是。

    傅里叶变换FT：将时间域函数转换为频率域函数；

    反傅里叶变换IFT：（反过来）将频率域函数转换为时间域函数。

    这里大家可能要问，什么叫时间域函数？什么又叫频率域函数呢？

图1：这个图是网上找的一个比较直观的反映傅里叶变换的图

    时间域函数简单来说就是以函数来描述随着时间变化，目标（信号强度，幅度.....）的变化的关系。

    频率域函数就是以函数来描述目标频率。

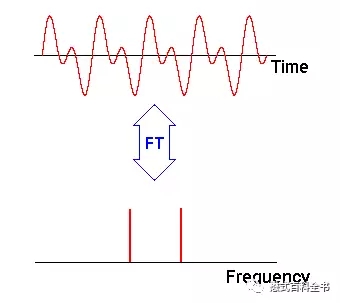
图2：图解傅里叶变换FT，上面为一个时间域函数，随时时间变化，信号的变化函数；下图为一个频率域函数，表示经过傅里叶变换后，该信号的频率。本例中可以看到，上面的信号随着时间变化呈周期性变化，信号形状不是标准的正弦曲线和余弦曲线，说明信号包含两种以上不同频率，经过FT后，把信号的频率分解出来。

   而磁共振图像则是通过反傅里叶变换（IFT），MR扫描的数据填充到K空间，利用K空间进行IFT得到磁共振图像。

   磁共振成像，采集的数据，为了空间定位，需要用到几个方向的的梯度对空间进行编码，我们采集得到的数据并不是时间域函数，而是频率域函数。所以，我们需要对K空间中的数据进行IFT，得到时间域函数，并且解析出每个质子的空间定位，得到磁共振图像。

   综合以上，磁共振图像的产生有三个主要步骤：

   1.通过RF脉冲和梯度磁场的配合使成像区域的质子产生信号（FID信号，SE信号，STE信号等）；

   2.利用磁共振线圈采集这些信号并且将采集的信号填充到K空间；

   3.对K空间中的数据进行IFT（实际上是有两次傅里叶变换FT和IFT），得到磁共振图像。

   1946年，布洛赫和珀塞尔分别独立的发现磁共振现象以来，当时磁共振现象到应用到医学领域还有一段路要走。1973年，Paul Lauterbur 劳特布尔发明了反投影磁共振成像法，利用磁共振做出了图像。但是这种方法很麻烦。1975年，Richard Ernst 厄恩斯特采用傅里叶变换的方法来进行磁共振图像成像，这种方法简单，准确，基本上后来的磁共振成像都是用到这种方法。

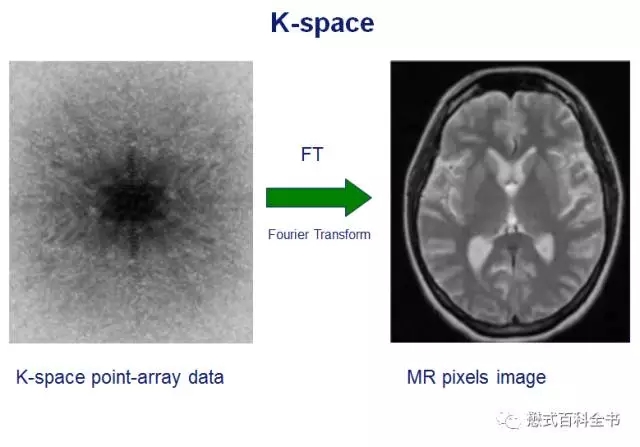
K空间的概述

    讲了这么多，大家只需要简单的记住，K空间就是储存磁共振原始数据的空间，可以通过K空间的原始数据进行非常复杂的数据后处理，得到磁共振图像。

    那么可能有老师要问，我们大部分人都是学医的，不是搞物理的或者搞数学的或者是搞图像后处理的，我们知道K空间有什么用呢？

    K空间有很多特性，了解了K空间的一些特性之后，我们可以更好的利用它的特点，做快速成像；另外，我们的很多科研及序列研发需要用到磁共振的原始数据，也需要用到K空间；有时候，磁共振图像出现了伪影，我们也可以通过调取出K空间，来查看是否有射频干扰，或者不相干的信号采集。

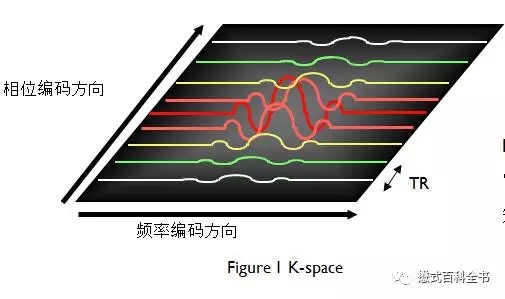
图3：上图是一个K-space的示意图

    上图是一个K空间的示意图，我们知道磁共振需要需要对质子进行空间定位，会用到不同方向的梯度磁场。

    如果以一个2D采集为例，首先通过层面选择梯度，激发某一固定的一层，然后在通过相位偏码梯度和频率编码梯度来对该层的质子进行空间定位。

    一个二维平面，我们可以把它分为两个正交方向，即：Ky（相位编码方向）和Kx（频率编码方向）。一个TR周期，把采集的一次信号填充到K空间中，在相位编码方向上，有多少个步级，我们就需要填充多少个相位编码线，最后把K空间数据填充完毕，进行图像后处理形成磁共振图像。

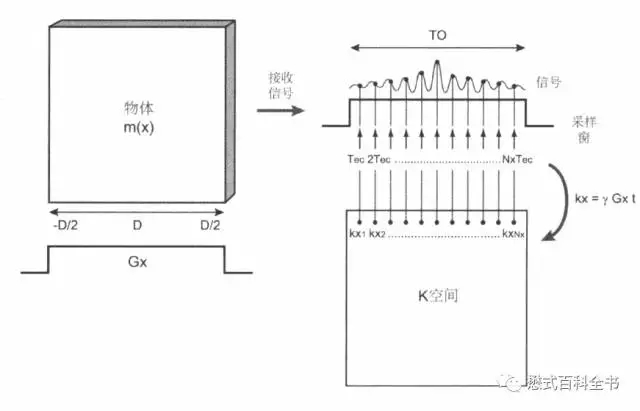
图4：频率编码梯度在采集接收信号的时候持续地施加，信号采样持续时间为Ts（图中为TO），频率编码梯度也持续到该过程结束。

    在MR图像采集过程中，每填充一条相位编码线，相位编码梯度都发生变化，而频率编码梯度并不变。

    相位编码梯度变化一次，进行质子的相位编码方向（Ky）的定位。在频率编码方向上，一次信号采集，会采集很多的采样点，作为频率编码方向（Kx）的定位。

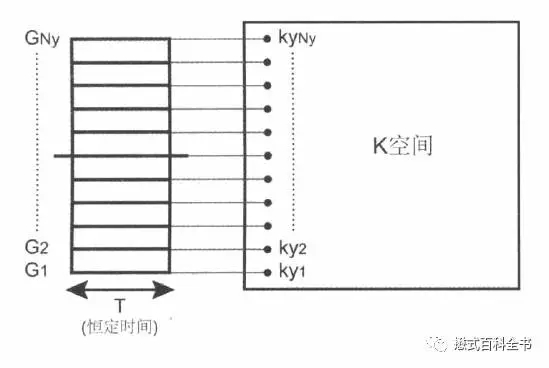
图5：相位编码梯度在采集信号之前就施加，施加了一定时间后，立即停止。这样保留了相位编码方向不同位置质子的相位差异。在信号采集的时候，相位编码梯度必须关闭。每一次相位编码梯度变化，采集一次信号，填充到一条相位编码线。

    所以，如果相位编码方向分辨率越高（矩阵越多，阵列越多），就等于采集的相位编码线越多，每一次填充一条相位编码线，相位编码梯度都会变化，都会经过一个TR时间，这样的话扫描时间就和相位编码步级（填充到K空间的相位编码线）有关。

    而在频率编码方向，一次采集的采样点越多，频率编码方向的阵列就越多，频率编码方向的分辨率越高。但是，一次采集，采样点多了，采集时间（Ts）并不会太明显的增加。所以，提高频率编码方向分辨率，有时候并不会增加扫描时间。

K空间的共轭对称性

    首先要了解的K空间的第一个特性就是共轭对称性。

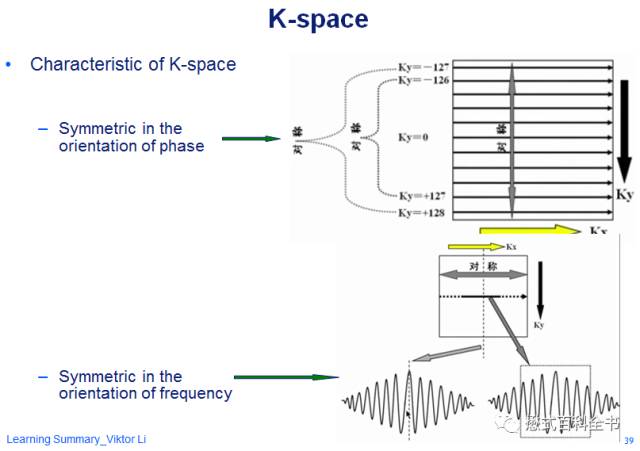
图6：K空间的共轭对称示意图

    这里什么叫共轭对称呢？共轭对称的意思是：当一个函数，它的实部为偶函数，虚部为奇函数的时候，并且满足f（x）=f（-x），这个函数就叫共轭对称函数。简单的说就是，把K空间分为四个象限的话，每个对角线都是对称的。

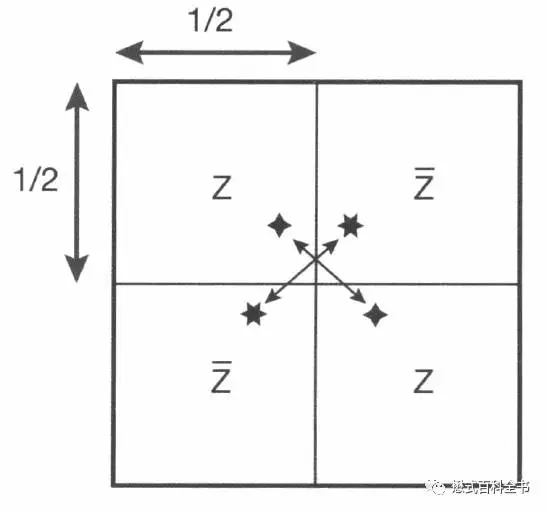
图7-8：K空间共轭对称示意图。

    K空间的对称性，其实理解起来也不难。在频率编码方向（Kx）方向，我们采集的是很多信号采样点，模拟成连续信号后，是一个对称的信号变化曲线。

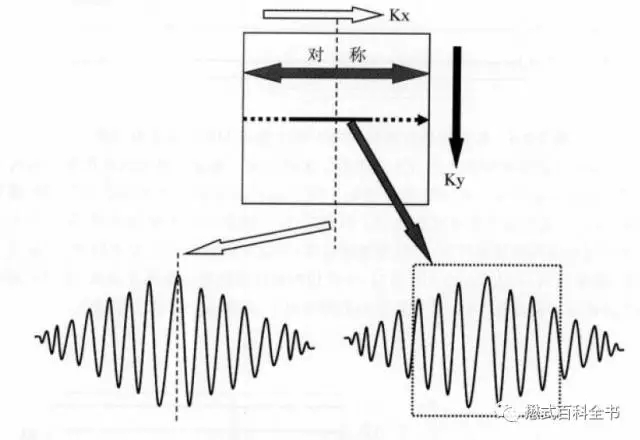图9：K空间频率编码方向的对称性

    相位编码方向也是对称的。因为每次相位编码梯度会变化，在K空间中心的时候，不施加相位编码梯度（相位编码梯度为0），在两边分别依次递增相位编码梯度，但是两边的方向相反，所以在相位编方向，K空间也是对称的。

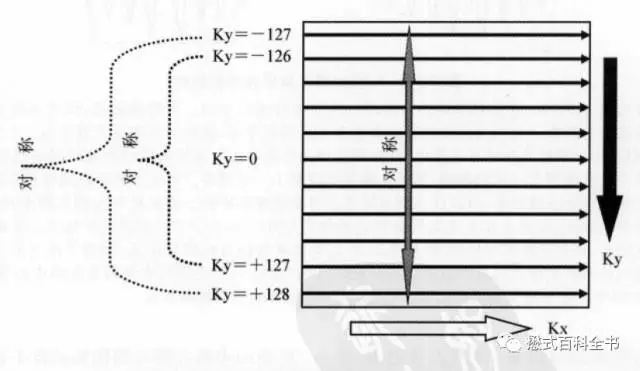
图10：相位编码方向上K空间的对称性

    利用K空间的对称性，我们可以做什么呢？当然是加速扫描了。因为，传统来说，我们要重建磁共振图像，得把K空间数据填满，特别是相位编码方向（因为相位编码步级决定扫描时间）；如果我们只填充一半相位编码线，这样的话，扫描时间就节约了，在利用K空间的共轭对称性，利用数学算法，算出K空间的另外一半，这样也可以重建图像。

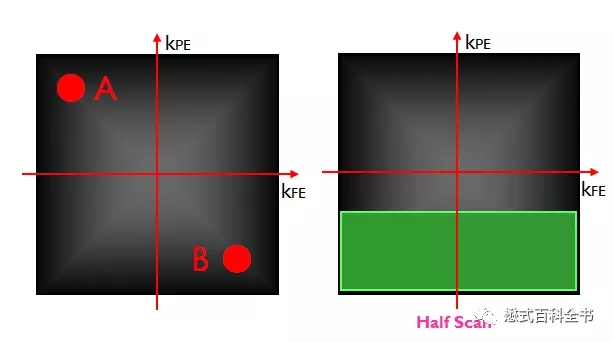
图11：利用K空间对称性，做快速扫描

    理论上，在相位编码方向（Ky），由于K空间相位编码方向的对称性，我们只需要填充一半的相位编码线，就可以利用数学算出另外一半，然后重建图像节约扫描时间。这种只填充K空间一半（一半以上）的相位编码线的方法叫做半扫描（部分K空间技术）。

    飞利浦中，半扫描叫做Half Scan；

    GE公司中，半扫描是怎么做的呢？把NEX（信号激励次数）采用小于1的就可以了；

    西门子公司中，半扫描叫做部分傅里叶技术，Phase Partial Fourier。

    同样，在频率编码方向（Kx），K空间也是对称的。在信号采集中，我们可以只采集一半（一半多一点）的信号，这样可以较少信号采样点来节约采样时间Ts，有可能会达到节约TR时间的目的。这种在频率编码方向利用对称性，减少采集时间的方法又叫做半回波技术（部分回波技术）。

    飞利浦中，部分回波技术，叫做Partial echo；

    西门子中，该技术叫Asymmetric echo；

    GE公司，这种技术叫在参数中，把TE改为最小Minimum TE，那么采集的回波是部分回波Fractional echo。

    当然，有老师肯定会问，既然K空间在频率编码方向和相位编码方向都是对称的，又是共轭对称的，我们是否可以只采集K空间的1/4（既K空间中的一个象限），就可以完成图像重建，这样可以大大的加速。理论上是这样的，但是实际扫描中，我们不会这样。大家可以注意，即使我们使用半扫描技术，我们也不会只填充K空间一半相位编码线，我们会填充稍微大于一半的相位编码线。这是为什么呢？

K空间的图像特性

    这里需要注意的是，K空间的每一点并不是和重建以后的图像的每一个体素一一对应的，了解这一点非常重要。

    K空间中，每一点上都包含了全部采集的磁共振信息。而重建以后的图像，每一个点对应一个体素，该体素只对应该点的信号强度信息。

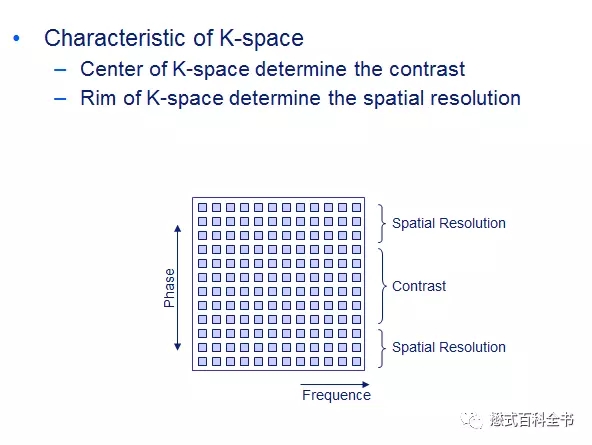
图12：K空间后处理后的图像特性

   K空间除了具有对称性的特点外，最重要的另一个特性就是后处理后的图像特性。

    K空间中心（中央）部分的数据，主要决定图像的对比度；

    K空间周边（周围）部分的数据，主要决定图像的细节（空间分辨率）。

    我们如何来证明这个呢！

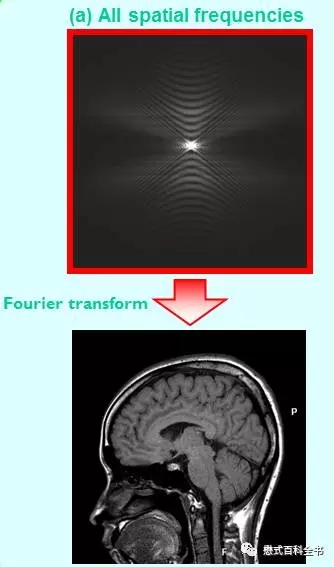
图13：把K空间所有的信息（中央部分和周边部分）都利用，重建后的图像是一个完整的图像。对比度和解剖细节都很好。

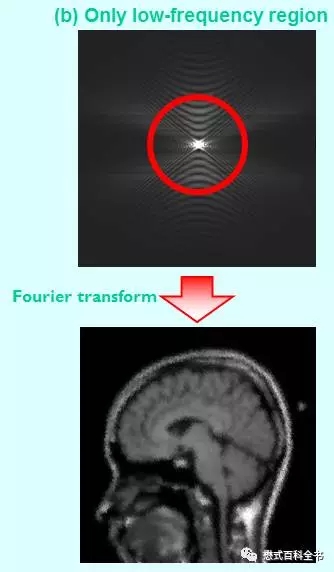
图14：只利用K空间中心部分数据来做图像重建，把周围数据丢弃掉。可以发现重建出来的图像，对比度比较好（基本上跟图13差不多），但是空间分辨率不够，解剖细节模糊。

图15：只利用K空间周边数据，把中心部分数据丢弃，来重建图像。可以发现，重建图例的图像，周围有轮廓，有解剖细节，但是没有对比度，无论是脑脊液和脑实质，还是灰质白质，都没有对比度。

    所以，知道上面的K空间特性后，我们也可以利用这一点来进行一些图像的加速或者消除运动伪影等。

K空间的填充轨迹

    这一部分我会在后面参数的故事（五）中讲到。我们前面讲了这么久的K空间，为了方便大家理解，我们都默认为K空间是遵循一种线性的次序填充的方式，也就是一条相位编码线填充完，再填充下一条线，再下一条，以此类推.....

    我们前面知道，K空间是存储磁共振原始采集数据的空间，利用K空间中的数据我们可以重建磁共振图像。那么只要保证K空间里的数据足够我们就能够得到磁共振图像。也就是不管用什么方式，只要保证K空间中填充有足够的数据就可以，所以我们可以并不拘泥于这种线性填充方式。我们还可以变换各种花样来填充K空间。

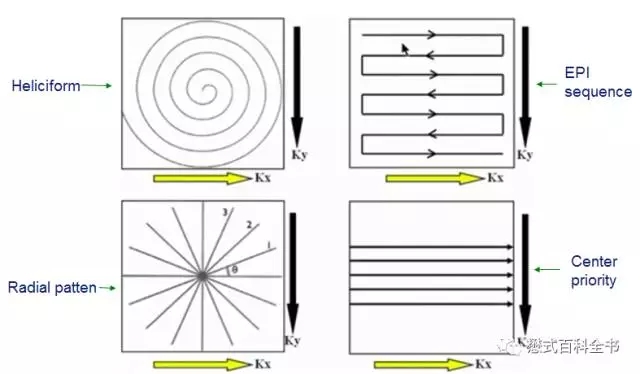
图16：不同轨迹的K空间填充方式

   有的老师可能会问，好好的线性填充方式，为什么要变换花样填充K空间呢！不同的K空间填充方式会有不同的作用。

    比如，采用放射状的填充方式，我们可以看到，每一次填充完一条相位编码线，相位编码梯度变化，旋转一下角度，再填充下一条相位编码线，这样的话，K空间中心部分会被反复的重复填充。因为K空间中心部分主要决定对比度，所以，通过这种方式填充，可以消除部分运动伪影。

K空间填充顺序

    除了K空间填充轨迹的不同，我们还可以对K空间填充顺序做出改变。我们前面讲的，K空间采用一条线一条线的填充。从周边先填充到中心，再填充到周边。这种方式是比较常用的线性填充方式。

    我们还可以，一开始就填充K空间中心部分，然后再分别往两边填充。这样的话，因为中心部分是决定图像对比度的，所以一开始扫描就填充K空间中心的话，会在做打药血管方面很有优势。

    后面讲参数，还会更详细的讲解，K空间填充顺序不同，对磁共振图像的对比度的影响。

总结

    最后总结一下K空间的一些基本特性。

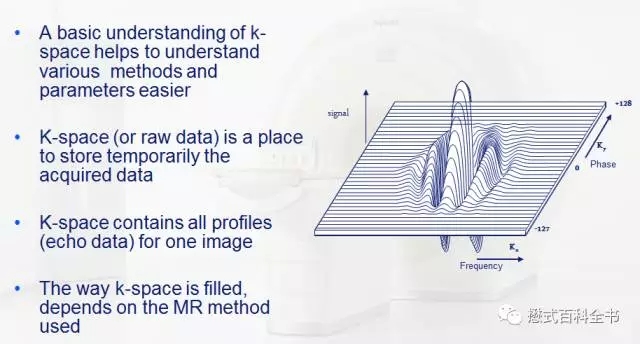
图17：总结K空间特性

   1.K空间中的阵列点并不是和重建后的图像像素点一一对应；

    2.K空间有共轭对称性，在相位编码方向上对称，在频率编码方向上也对称；利用K空间对称性，我们可以减少K空间的填充，利用数学方法算出另外的数据，这样可以进行磁共振成像的加速；

    3.K空间中心部分数据主要决定图像对比度；K空间周边部分数据主要决定图像的空间分辨率。利用这些特性，可以通过变换K空间填充顺序和填充轨迹进行运动伪影的消除或精确的抓准血管成像时间；

    4.K空间的填充轨迹有很多方法，不同填充轨迹，会有不同的作用；

    5.K空间填充的顺序也有不同，不同的填充顺序可以决定图像的对比度。

    所以，K空间有这么多作用，真是了不起啊！

该少侠的其他优雅清秀，质朴华丽的文章，大气中带着婉约，突出尊贵体验（老规矩，点击就送）：

磁共振2D和3D扫描序列的区别

第一次转载文章，就转的这么硬核，好炫彩，好夺目，（戏说不是胡说、改版不是乱编），2019年，中中合开的思影科技脑影像数据处理课程就要开始了，还不直接点击？这么巧，你也在关注思影科技啊：

第十三届功能磁共振数据处理基础班（万事开头难，这只是开始，勇敢挑战自我）

第八届磁共振脑网络数据处理班（脑网络，多高大上啊）

第三届动物磁共振脑影像数据处理班 （这么巧，你也有7t和9.4t磁共振啊？）

第三届脑功能磁共振提高班暨任务态fMRI专题班（激活！）

第十四届功能磁共振数据处理基础班（在南京）

第二届脑影像机器学习班（这年头不整整AI,出门都不好意思跟人打招呼）

第三届脑影像机器学习班（在南京出门跟人打招呼）

第五届磁共振脑影像结构班（来自全代码linux的酸爽快乐）

第七届磁共振弥散张量成像数据处理班（酸爽+1）

第四届磁共振ASL（动脉自旋标记）数据处理班（不打药，真不打药！）

思影数据处理业务一：功能磁共振（fMRI）（不挣钱，为了情怀）

思影数据处理业务二：结构磁共振成像(sMRI)与DTI（数据处理哪家强？思影科技就是刚！）

思影数据处理业务三：ASL数据处理（你能提出cbf吗？）

思影数据处理业务四：EEG/ERP数据处理（全手工代码制作，匠人精神）

招聘：脑影像数据处理工程师-南京（你将免费获得一次提高自我的机会，永不加班！）