最近不少读者对高大上的机器学习,动态脑网络,曲面形态指标共变网络感到爱不起,针对于此,我们特别推出一些基本的做脑功能的概念讲解,希望大家一步一步来,年轻人,不要动不动想一步登天,识得唔识得啊?
<!--[if !supportLineBreakNewLine]-->
<!--[endif]-->
那今天我们就谈谈这个相关系数…….
说起相关系数,从字面上的含义就可看出,就是两个信号之间的相关性。但是你真正理解内在的机理吗?
结论放在最前面:相关系数,其实就是通过散点图来的。
学会散点图,此生无憾!
所有的一切,由这个图说起:
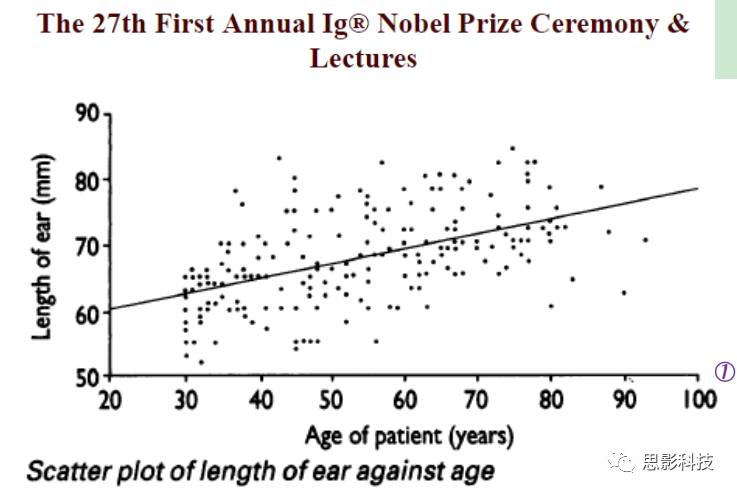
图1:Ref: JamesAH, BMJ, 1995, 311: 1668.
有一个人,他测量了一组人的“量表”。其中这个“量表”包含着年龄和耳朵长度。这样子他就得到一个二维小表格如下图示:
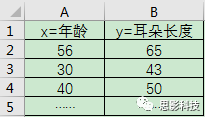
图2:萌萌哒的二维量表小表格
然后他在坐标纸上面进行打点,X轴坐标设置为年龄,y轴坐标设置为耳朵长度。然后每一行就是一个点,也就是说:每一个点对应着一个被试信息。
紧接着,他就拿手来比划,画出一根能最好拟合这个散点趋势的线(拟合或最小二乘法)。这样他就发现:年龄越大,耳朵越长。Ps:怪不得如来佛耳朵如此长,连起来可以绕地球一圈。
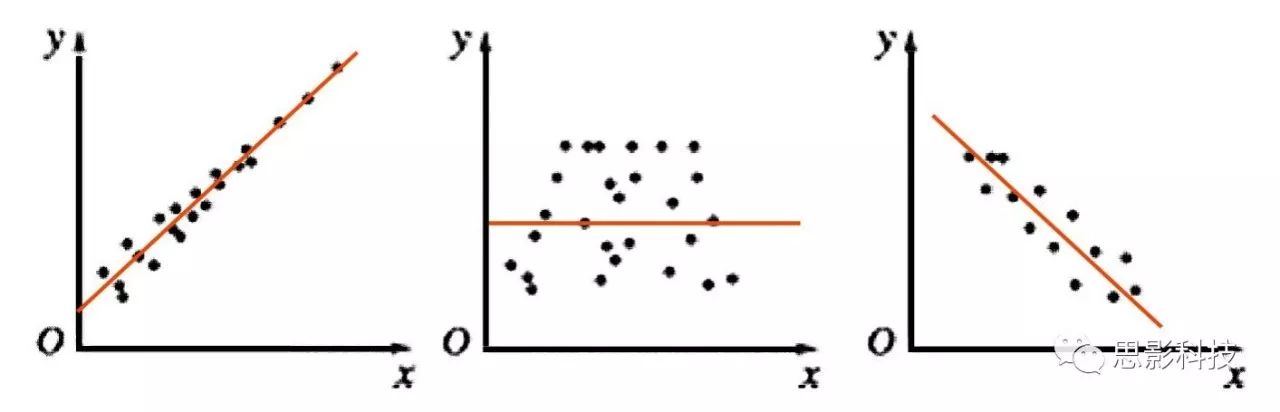
图3:散点图与拟合线(橙色),左:正相关;中:不相关;右:负相关
其实我告诉你,现在这根橙色拟合线的趋势就是相关性。如果这根线是朝着右上角走,就是正相关;如果这根线是朝着右下角走,就是负相关;如果这根线水平,就代表着不相关。
但是理想很美好,现实很残酷。真正拿到数据进行计算相关系数,多多少少会存在一定的相关性,真正不相关的例子太少太少,(比如你和思影科技,你来参加培训,于是我们就相关了,培训信息还是老规矩翻看历史信息或简单粗暴的点击阅读原文,你没看错,此处还是广告,惊喜不惊喜?意外不意外?)。前一阵子有一篇文章说:中国三峡大坝是影响日本地震的原因。该文说这个相关性还是非常非常显著的。
那么问题来了:相关系数的计算怎么会有显著性呢?
多图警示!

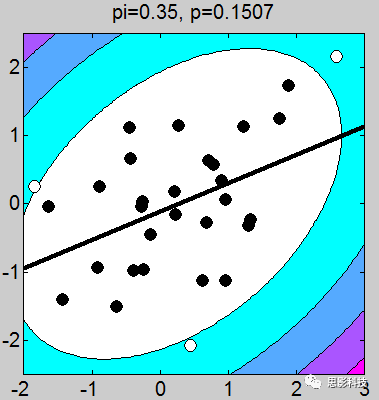

我做了一堆图,上面的这个例子取得不够恰当,我应该让这些图拟合的斜率是一致的(相关系数一致),但是不要在意这些细节。小伙伴们有没有看到图上的P值,那个p值就是相关的显著性。我们可以很轻松的发现:只要散点的点,越靠近拟合曲线,那么显著性越强。散点越分散,显著性越差。
以上几点细节部分特此做一个说明:
1、画散点图的时候,有白点,有黑点。图中的白点是剔除的,黑点是选取的。
2、剔除点是根据三倍方差以上的点进行剔除(图中色彩斑斓的圈,就是n倍方差边界线)
3、相关系数和斜率存在一定关系,可以说,斜率越靠近1,相关系数越大。(相关系数取值-1~1),其中0代表不相关,1代表正相关,-1代表负相关。
4、最佳拟合线的画法:在这里三种方法是等价关系,得到的数值是一样的。(最小二乘法 = 一次拟合 = 一次回归)
5、本文所指相关,指代皮尔逊相关,

没错就是他:卡尔·皮尔逊
<!--[if !supportLineBreakNewLine]-->
<!--[endif]-->
(眼神里透露着浓浓的英伦学者风,一口倍地道的伦敦腔“May I help you,sir?)
不对,应该是它:

其中:
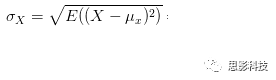
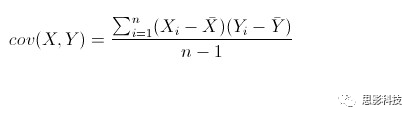
皮尔逊相关ρ,协方差Cov(x,y),标准差σx σy
注:在公式内并无显著性水平计算,显著性解释是作者领悟的。在matlab中,计算相关系数是有显著性输出的。此显著性并未通过多重比较较正。有关校正,敬请看后面推送。
现在说了这么多,让我来告诉你,一些在脑科学领域用散点图来解释的本质:
1、功能连接:功能连接最早的定义就是皮尔逊相关,而功能连接就是两个脑区时间点的散点图
2、结构上的协变连接:协变连接是用得最早的,在磁共振出现之前,前人研究PET(PET表示高贵的我,一般人做不起)就是采用协变连接。简单说,就是A、B两个脑区之间的散点图。
3、回归:有没有发现回归也是这样子的?
